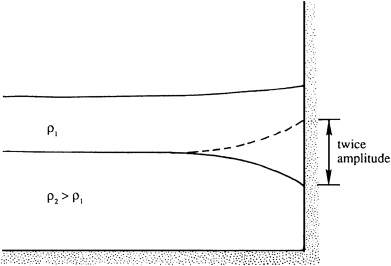
Internal Kelvin Waves
Analogous to the surface or “external” Kelvin waves discussed in the preceding paragraphs, internal Kelvin waves at the interface between two fluids of different densities can also exist
InternalKelvinWave

If the lower layer is very deep, then the speed of propagation is \(c = [g'H]^{1/2}\) where \(H\) is the thickness of the upper layer and \(g' = g(\rho_2 - \rho_1)/\rho_2\) is the reduced gravity.
For a continuously stratified medium of depth \(H\) and buoyancy frequency \(N\), internal Kelvin waves can propagate at any of the normal mode speeds 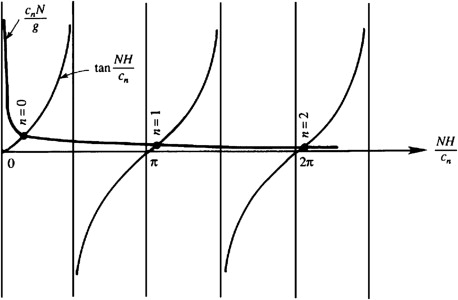EigenvalueMode given by \(\boxed{\tan\left( \frac{NH}{c_n} \right) = 0 \Rightarrow c_n = \frac{NH}{n\pi} \quad \text{for} \quad n = 1, 2, 3, \dots}\)

The decay scale for internal Kelvin waves is again \(\boxed{\Lambda = c/f}\), but it is called the internal Rossby radius of deformation. The value of \(\Lambda\) for internal Kelvin waves is much smaller than the external Rossby radius of deformation.
For \(n = 1\), a typical value in the ocean is \(\Lambda = NH/\pi f \sim 50 \, \text{km}\) a typical atmospheric value is much larger, being of order \(\Lambda \sim 1000 \, \text{km}\)

◀ ▶