If a point in a large water tank is rapidly tilted and some water spills out, it will generate outward motion and waves. In a sufficiently large body of water—such as the rotating ocean on Earth—after some outward motion, the Coriolis force turns the water’s motion by 90°, preventing it from continuing to move outward. The condition under which this situation typically occurs defines the Rossby radius of deformation. It balances the acceleration due to pressure gradient and gravity against the Coriolis acceleration (i.e., the Coriolis “force”) on Earth’s rotating surface.
Put simply, the Rossby radius of deformation acts like a boundary limit: the width of a disturbance cannot exceed this characteristic scale. This concept helps explain "why the width of coastal Kelvin waves increases near the equator", because the Coriolis parameter \(f\) becomes smaller near the equator. Since the Rossby radius is inversely proportional to \(f\), it increases as one moves equatorward.
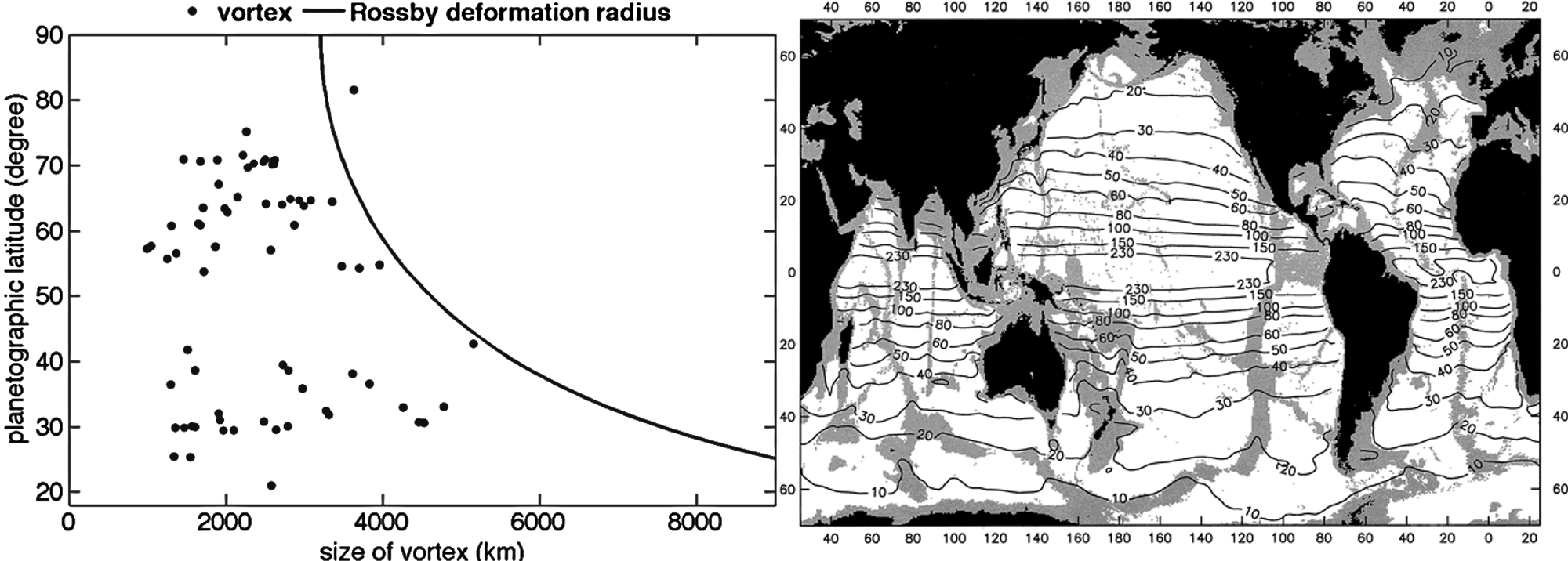
1 Chelton, D. B., R. A. deSzoeke, M. G. Schlax, K. El Naggar, and N. Siwertz, 1998: Geographical Variability of the First Baroclinic Rossby Radius of Deformation. J. Phys. Oceanogr., 28, 433–460,
https://doi.org/10.1175/1520-0485(1998)028<0433:GVOTFB>2.0.CO;2
2Trammell, Harold et al. (2016). Vortices in Saturn's Northern Hemisphere (2008-2015) Observed by Cassini ISS: Vortices in Saturn's NH from Cassini ISS. Journal of Geophysical Research: Planets. 121. 10.1002/2016JE005122.