If \( \delta S \) is an infinitesimal surface element whose normal points in the direction of the unit vector \( \hat{\mathbf{n}} \)
\begin{equation}
\hat{\mathbf{n}} \cdot (\nabla \times \mathbf{u}) = \frac{1}{\delta S} \oint_{\delta r} \mathbf{u} \cdot d\mathbf{r}
\end{equation}
where the line integral is around the infinitesimal area. Thus at a point the component of vorticity in the direction of \( \mathbf{n} \) is proportional to the circulation around the surrounding infinitesimal fluid element, divided by the elemental area bounded by the path of the integral
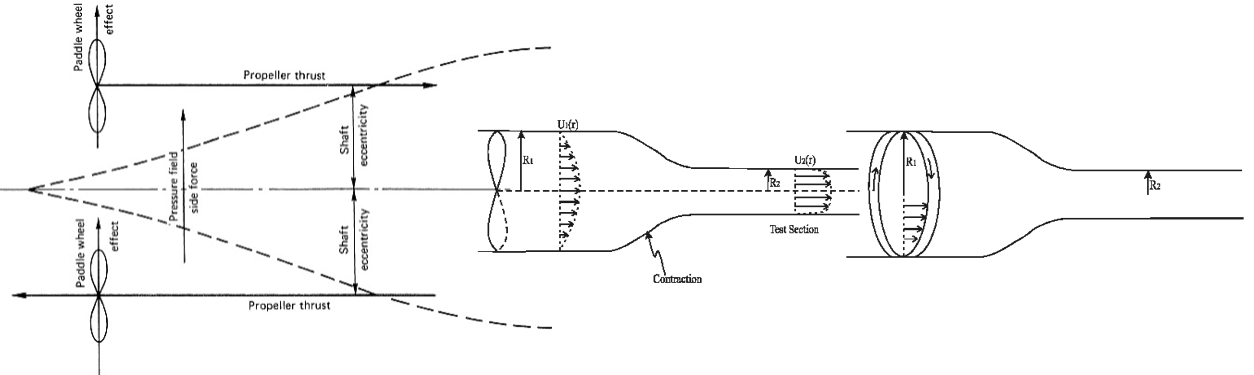
A heuristic test for the presence of vorticity is to imagine a small paddle wheel in the
flow; the paddle wheel acts as a ‘circulation-meter’, and rotates if the vorticity is non-zero.
Vorticity might seem to be similar to angular momentum, in that it is a measure of spin.
However, unlike angular momentum, the value of vorticity at a point does not depend on the
particular choice of an axis of rotation; indeed, the definition of vorticity makes no reference
at all to an axis of rotation or to a coordinate system. Rather, vorticity is a measure of the
local spin of a fluid element.
- If the paddle wheel is rotating clockwise then there is negative (or anticyclonic) relative vorticity.
- If the paddle wheel is rotating counter-clockwise then there is positive (or cyclonic) relative vorticity.