Large-scale geophysical flows are almost always influenced by vorticity, and the change of \(\omega\) due to the presence of planetary vorticity \(2\Omega\) is a central feature of geophysical fluid dynamics.

Kelvin’s circulation theorem for inviscid flow in a rotating frame of reference is modified to \[\frac{D \overbrace{\Gamma_a}^{\text{circulation due to absolute vorticity}}}{D t} = 0\] \[ \Gamma_a \equiv \int_A \underbrace{\bigl(\overbrace{\boldsymbol{\omega}}^{\text{vorticity}} + \overbrace{2\boldsymbol{\Omega}}^{\text{planetary vorticity}}\bigr)}_{\text{absolute vorticity}} \cdot \mathbf{n} \, dA = \underbrace{\Gamma}_{\text{original circulation}} + 2 \int_A \underbrace{\boldsymbol{\Omega} \cdot \mathbf{n}}_{\text{planetary vorticity intersected by } A} \, dA\]

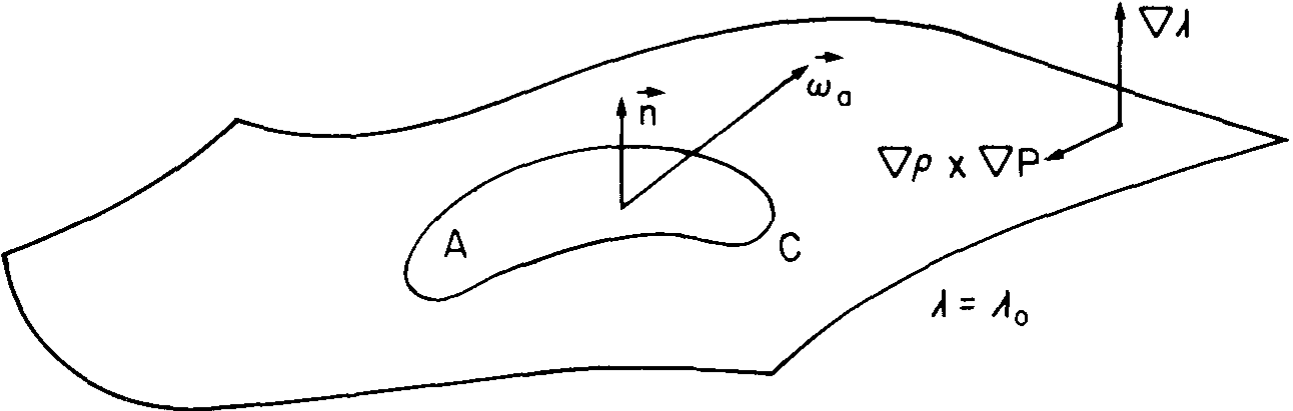
If the flow is baroclinic, Kelvin’s theorem is not conserved: \( \frac{d \Gamma_a}{dt} = \oint_C \frac{1}{\rho^2} \nabla \rho \times \nabla p \cdot d\mathbf{l} \)
Using Stokes’ theorem:\( \begin{aligned} &\oint_C \mathbf{u} \cdot d\mathbf{l} = \iint_A \nabla \times \mathbf{u} \cdot \mathbf{n} \, dA \\ \qquad &\qquad \qquad \Downarrow \\ &\frac{d}{dt} \iint_A \boldsymbol{\omega}_a \cdot \mathbf{n} \, dA = \iint_A \frac{\nabla \rho \times \nabla p}{\rho^2} \cdot \mathbf{n} \, dA \end{aligned} \)

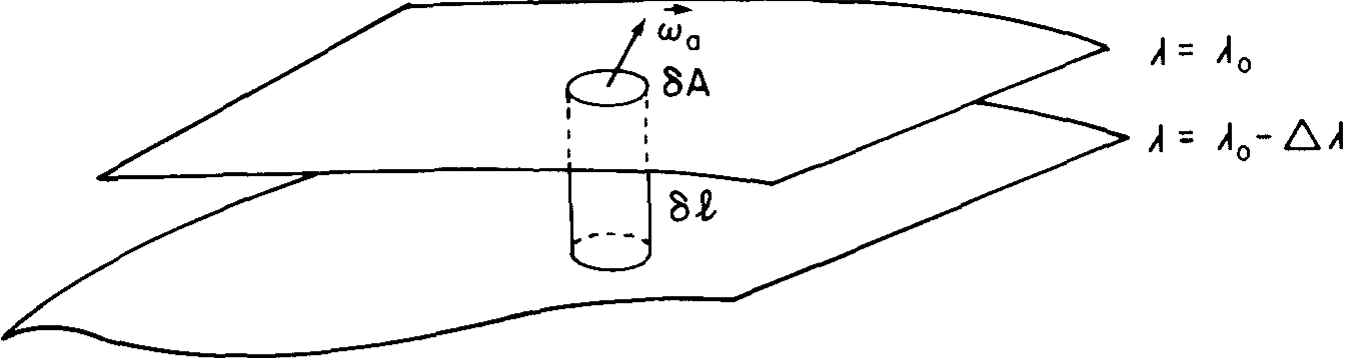
Consider a tiny circuit \(C\) which is sufficiently small \[\frac{d}{dt}(\boldsymbol{\omega}_a \cdot \mathbf{n} \, \delta A) = 0 \] in the surface of constant \(\lambda\), \(\delta A\) is the small surface element enclosed by \(C\), and \(\boldsymbol{\omega}_a\) is the mean value of \(\boldsymbol{\omega}_a\) over the differential surface

¹ Pedlosky, J. (1982). Geophysical Fluid Dynamics. Springer study edition. Springer, Berlin, Heidelberg.

◀ ▶