Rewrite the curl operation in index notation and apply Gauss’ divergence theorem \[ \int_{V'} \nabla' \times \left( \frac{\boldsymbol{\omega}(\mathbf{x}', t)}{|\mathbf{x} - \mathbf{x}'|} \right) \, d^3x' = \int_{V'} \varepsilon_{kij} \frac{\partial}{\partial x'_i} \left( \frac{\omega_j(\mathbf{x}', t)}{|\mathbf{x} - \mathbf{x}'|} \right) d^3x' = \int_{A'} \varepsilon_{kij} \left( \frac{\omega_j(\mathbf{x}', t)}{|\mathbf{x} - \mathbf{x}'|} \right) n_i \, d^2x' \]

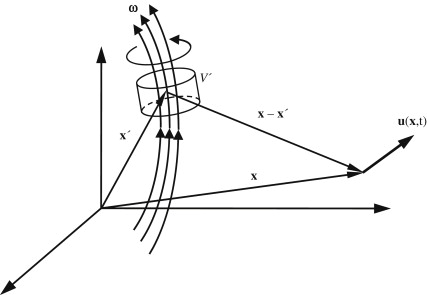
\(A'\) is the surface of \(V'\) and \(\mathbf{n}\) is the outward normal on \(A'\). Choose \(V'\) to be a volume aligned so that its end surfaces are locally normal to \(\boldsymbol{\omega}(\mathbf{x}', t)\) while its curved lateral surface lies outside the concentration of vorticity. For this volume, the final integral in the equation above is zero because \(\mathbf{n} \times \boldsymbol{\omega} = 0\) on its end surfaces since \(\boldsymbol{\omega}(\mathbf{x}', t)\) and \(\mathbf{n}\) are parallel there, and because \(\boldsymbol{\omega}(\mathbf{x}', t) = 0\) on its lateral surface The same result may be achieved when \(\boldsymbol{\omega}(\mathbf{x}', t)\) is nonzero on the volume's lateral surfaces when the integrand is self-canceling on the volume's lateral surfaces. In either case, \(\mathbf{u}(\mathbf{x}, t)\) reduces to: \[ \mathbf{u}(\mathbf{x}, t) = \frac{1}{4\pi} \int_{V'} \frac{\boldsymbol{\omega}(\mathbf{x}', t) \times (\mathbf{x} - \mathbf{x}')}{|\mathbf{x} - \mathbf{x}'|^3} \, d^3x' \]

Further specialized to a slender vortex element of length \(dl\) by choosing \(V' = \Delta A' dl\) \[ d\mathbf{u}(\mathbf{x}, t) \cong \frac{1}{4\pi} \int_{\Delta A'} |\boldsymbol{\omega}(\mathbf{x}', t)| \, \mathbf{e}_{\omega} \, d^2x' \times \frac{(\mathbf{x} - \mathbf{x}')}{|\mathbf{x} - \mathbf{x}'|^3} \, dl = \frac{\Gamma \, dl}{4\pi} \, \mathbf{e}_{\omega} \times \frac{(\mathbf{x} - \mathbf{x}')}{|\mathbf{x} - \mathbf{x}'|^3} \] \[ \underbrace{\mathbf{u}(\mathbf{x}, t)}_{\substack{\text{velocity induced by}\\ \text{the entire slender vortex}}} = \int_{\text{vortex}} \underbrace{d\mathbf{u}}_{\substack{\text{velocity induced by an}\\ \text{element of the slender vortex}\\ \text{having length } dl}} \cong \frac{ \overbrace{\Gamma}^{\substack{\text{strength of}\\ \text{the vortex element}\\ \text{at } \mathbf{x}'}} }{4\pi} \int_{\text{vortex}} \underbrace{\mathbf{e}_{\omega}}_{\substack{\text{direction of}\\ \text{the vortex element}\\ \text{at } \mathbf{x}'}} \times \frac{(\mathbf{x} - \mathbf{x}')}{|\mathbf{x} - \mathbf{x}'|^3} \, dl \] These are expressions of the Biot–Savart vortex induction law

This gives the velocity field when the vorticity distribution \(\boldsymbol{\omega}(\mathbf{x}')\) is known. Originally, this law was given for a magnetic field (in place of \(\mathbf{u}\)) produced by steady electric current (in place of \(\boldsymbol{\omega}\)) of volume distribution in the electromagnetic theory.

◀ ▶