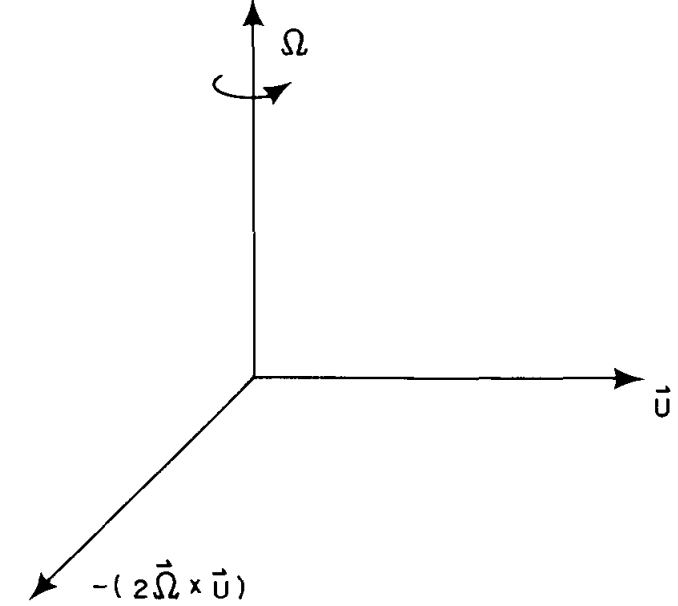
If the Coriolis acceleration term is moved to the right-hand side of \(\rho \left[ \frac{d\mathbf{u}}{dt} + 2\boldsymbol{\Omega} \times \mathbf{u} \right] = -\nabla p + \rho \nabla \Phi + \mathcal{F}\), it appears to an observer in the rotating frame as an additional force: the Coriolis force
The Coriolis force is always perpendicular to the velocity and thus does no work.
For an observer aligned with \( \boldsymbol{\Omega} \), the Coriolis force \( -2\boldsymbol{\Omega} \times \mathbf{u} \) acts to deflect moving fluid elements to their right.
The total time rate of change of any scalar, such as the temperature, is the same in rotating and nonrotating frames. The conservation of mass equation \(\frac{d\rho}{dt} + \rho \nabla \cdot \mathbf{u} = 0\) and the first law of thermodynamics equations \(\rho \frac{de}{dt} = -p \rho \frac{d}{dt} \rho^{-1} + k \nabla^2 T + \chi + \rho Q \) through \(\frac{dS}{dt} = F(S) \) are unaffected by the choice of coordinate frame and can be directly applied to a rotating coordinate system. Although the total derivative of a scalar is the same in both frames, the individual components of the substantial derivative are not invariant. For any scalar property \( P \) \[ \left( \frac{\partial P}{\partial t} \right)_I = \left( \frac{\partial P}{\partial t} \right)_R - (\boldsymbol{\Omega} \times \mathbf{r}) \cdot \nabla P \] while \[ \mathbf{u}_I \cdot \nabla P = (\mathbf{u}_R + \boldsymbol{\Omega} \times \mathbf{r}) \cdot \nabla P \] from which it follows that \[ \left( \frac{dP}{dt} \right)_I = \left( \frac{dP}{dt} \right)_R \]
1 Pedlosky, J. (1982). Geophysical Fluid Dynamics. Springer study edition. Springer, Berlin, Heidelberg.