\[ \rho \left( \frac{D'\mathbf{u}'}{Dt} \right)_{O'1'2'3'} = -\nabla' p + \rho \left[ \mathbf{g} - \frac{d\mathbf{U}}{dt} - 2\boldsymbol{\Omega} \times \mathbf{u}' - \frac{d\boldsymbol{\Omega}}{dt} \times \mathbf{x}' - \boldsymbol{\Omega} \times (\boldsymbol{\Omega} \times \mathbf{x}') \right] + \mu \nabla'^2 \mathbf{u}' \]

There are four new terms transforming from an inertial to a rotating (non-inertial) reference frame. These are additional terms that arise in the rotating frame compared to the classical Newtonian acceleration observed in the inertial frame.
The first new term \( \boxed{\frac{d\mathbf{U}}{dt}} \) accounts for the acceleration of \( O' \) relative to \( O \). An aircraft that is flown on a parabolic trajectory produces weightlessness in its interior when its acceleration \( \frac{d\mathbf{U}}{dt} = \mathbf{g}\)

The second new term is the Coriolis term depends on the fluid particle’s velocity, not on its position. Even at the earth’s rotation rate of one cycle per day, it has important consequences for the accuracy of artillery and for navigation during air and sea travel. The earth’s angular velocity vector \(\boldsymbol{\Omega}\) points out of the ground in the northern hemisphere. The Coriolis acceleration \(\boxed{ -2\boldsymbol{\Omega} \times \mathbf{u}} \) therefore tends to deflect a particle to the right of its direction of travel in the northern hemisphere and to the left in the southern hemisphere

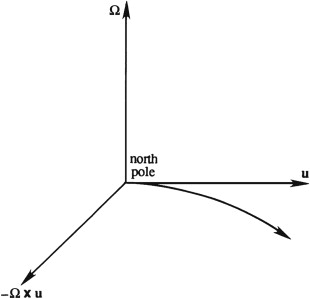
Imagine a low-drag projectile shot horizontally from the north pole with speed \( u \). The Coriolis acceleration \( 2\boldsymbol{\Omega} u \) constantly acts perpendicular to its path and therefore does not change the speed \( u \) of the projectile. The forward distance traveled in time \( t \) is \( ut \), and the deflection is \( \Omega ut^2 \). The angular deflection is \( \Omega ut^2 / ut = \Omega t \), which is the earth’s rotation in time \( t \). This demonstrates that the projectile in fact travels in a straight line if observed from outer space (an inertial frame)