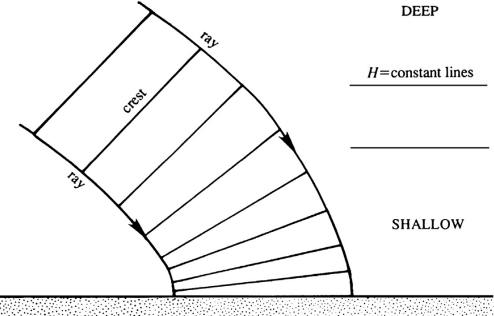
Consider a sloping beach, with depth contours parallel to the coastline. Assume that waves are propagating toward the coast from the deep ocean with their crests at an angle to the coastline. Sufficiently near the coastline they begin to feel the effect of the bottom and finally become shallow-water waves. Their frequency does not change along the path, but their speed of propagation \(\boxed{c = \sqrt{gH}}\) and their wavelength \( \lambda \) become smaller. The crest lines which are perpendicular to the local direction of \( c \) tend to become parallel to the coast. This is why the waves coming toward a gradually sloping beach always seem to have their crests parallel to the coastline.

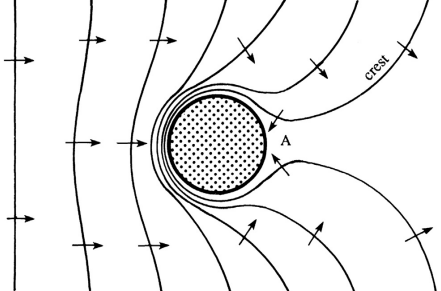
An interesting example of wave refraction occurs when a deep-water wave train with straight crests approaches an island. Assume that the water gradually becomes shallower as the island is approached, and the constant depth contours are circles concentric with the island. The waves always come in toward the island, even on the shadowed-side marked A.
The bending of wave paths in an inhomogeneous medium is called wave refraction. In this case the source of inhomogeneity is the spatial dependence of \( H \). The analogous phenomenon in optics is the bending of light due to refractive index changes along its path.