In addition to the kinematic condition at the surface, there is a dynamic condition that the pressure just below the liquid surface be equal to the ambient pressure, with surface tension neglected. Taking the ambient air pressure above the liquid to be a constant atmospheric pressure, the dynamic surface condition can be stated \[ (p)_{z = \eta} = 0 \] where \( p \) is the gauge pressure

When the flow is inviscid and surface tension is neglected it follows the conservation of momentum boundary condition \(\dot{m}_s \, (\mathbf{u}_2 - \mathbf{u}_1) \cdot \mathbf{n} = - (p_2 - p_1) + \left( (n_i \tau_{ij})_2 - (n_i \tau_{ij})_1 \right) n_j + \sigma \left( \frac{1}{R'} + \frac{1}{R''} \right)\), this equation above and the neglect of any shear stresses on \( z = \eta \) define a stress-free boundary. The water surface in this ideal case is commonly called a free surface

For consistency, this condition should also be simplified for small-slope waves by dropping the nonlinear term \( |\nabla \phi|^2 \) in the relevant Bernoulli equation \(\frac{\partial \phi}{\partial t} + \frac{1}{2} |\nabla \phi|^2 + gz + \frac{p}{\rho} = \text{constant}\): \[ \frac{\partial \phi}{\partial t} + \frac{p}{\rho} + gz \cong 0 \] where the Bernoulli constant has been evaluated on the undisturbed liquid surface far from the surface wave

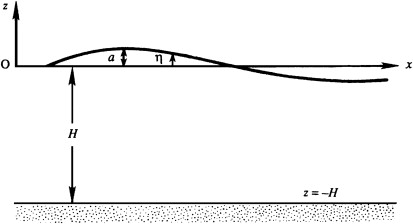
The Bernoulli constant has been evaluated on the undisturbed liquid surface far from the surface wave. Evaluating \(\frac{\partial \phi}{\partial t} + \frac{p}{\rho} + gz \cong 0\) on \( z = \eta \) and applying \((p)_{z = \eta} = 0\) produces \[ \left( \frac{\partial \phi}{\partial t} + \frac{p}{\rho} + gz \right)_{z = \eta} \cong \left( \frac{\partial \phi}{\partial t} \right)_{z = 0} + g \eta \cong 0, \quad \text{or} \quad \left( \frac{\partial \phi}{\partial t} \right)_{z = 0} \cong -g \eta \] The first approximate equality follows because \( \boxed{(\partial \phi / \partial t)_{z = 0}} \) is the first term in a Taylor series expansion of \( (\partial \phi / \partial t)_{z = \eta} \) in powers of \( \eta \) about \( \eta = 0 \)
It is consistent with \(\boxed{\left( \frac{\partial \phi}{\partial z} \right)_{z = 0} \cong \frac{\partial \eta}{\partial t}}\) for the kinematic boundary condition

◀ ▶