Starting from the ideal flow, properties of small-slope, small-amplitude gravity waves on the free surface of a constant-density liquid layer with uniform depth \( H \) can be derived. The depth \( H \) can be large or small relative to the wavelength \( \lambda \)

The limitation to waves with small slopes and amplitudes implies \( a/\lambda \ll 1 \) and \( a/H \ll 1 \). These two conditions allow the problem to be linearized

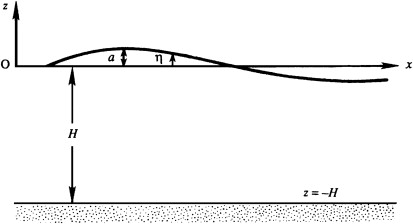
Choose the x-axis in the direction of wave propagation with the z-axis vertical so that the motion is two-dimensional in the x-z plane. Let the surface’s vertical deflection or waveform \( \eta(x,t) \) denote the vertical liquid-surface displacement from its undisturbed location \( z = 0 \)
Because the liquid’s motion is irrotational, a velocity potential \( \phi(x, z, t) \) can be defined \(\boxed{ u = \partial \phi / \partial x, w = \partial \phi / \partial z} \) so the incompressible continuity equation \( \partial u / \partial x + \partial w / \partial z = 0 \) implies \(\boxed{ \partial^2 \phi / \partial x^2 + \partial^2 \phi / \partial z^2 = 0} \)

There are three boundary conditions.

◀ ▶