• If \( \sigma > 0 \), the two media (fluids) are immiscible and \( A \) will reach a local minimum value at equilibrium
• If \( \sigma < 0 \), corresponding to surface compression, the two fluids mix freely since the minimum free energy will occur when \( A \) has expanded to the point that the spacing between its folds reaches molecular dimensions and the two-fluid system has uniform composition

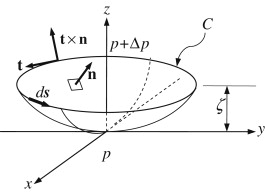
When \( \sigma > 0 \), minimum interface area is achieved by pressure forces that cause fluid elements to move. These pressure forces are determined by \( \sigma \) and the local curvature of the interface, the pressure above a curved interface is higher than that below it by an increment \( \Delta p \), and the shape of the fluid interface is given by \( \eta(x,y,z) = z - h(x,y) = 0 \)

The origin of coordinates and the direction of the z-axis are chosen so that \( h, \partial h / \partial x, \) and \( \partial h / \partial y \) are all zero at \( \mathbf{x} = (0,0,0) \). Plus, the directions of the x- and y-axes are chosen so that the surface’s principal radii of curvature, \( R_1 \) and \( R_2 \) are found in the x–z and y–z planes. The surface’s shape is given by \[ \eta(x,y,z) = z - \left( \frac{x^2}{2R_1} \right) - \left( \frac{y^2}{2R_2} \right) = 0 \] A closed curve \( C \) is defined by the intersection of the curved surface and the plane \( z = \zeta \)