From Leibniz's Theorem to the Reynolds Transport Theorem

Expressing \( \Delta V \) in Terms of the Surface Integral: Starting with the time derivative of the integral over the control volume: \[ \frac{d}{dt} \int_{V^*(t)} F(\mathbf{x},t) \, dV = \lim_{\Delta t \to 0} \frac{1}{\Delta t} \left\{ \int_{V^*(t)} \Delta t \frac{\partial F(\mathbf{x},t)}{\partial t} \, dV + \int_{\Delta V} F(\mathbf{x},t) \, dV \right\} \]

To evaluate the total time derivative of the integral over a moving control volume, express the volume increment as: \( \Delta V = V^*(t+\Delta t) - V^*(t) \)

Since small element of \( \Delta V \) is located adjacent to the surface \( A^*(t) \), approximate it using: \( \Delta V \approx (\mathbf{b} \Delta t) \cdot \mathbf{n} dA \), where:

  • \( \mathbf{b} \) is the velocity of the moving surface \( A^*(t) \),
  • \( \mathbf{n} \) is the outward normal to \( A^*(t) \).

Evaluating the Integral over \( \Delta V \): Using the volume increment approximation, the integral \( \int_{\Delta V} F(\mathbf{x},t) dV \) can be rewritten as: \( \int_{\Delta V} F(\mathbf{x},t) dV = \int_{A^*(t)} F(\mathbf{x},t) (\mathbf{b} \Delta t \cdot \mathbf{n}) dA\)

All these elemental contributions to ΔV may be summed together via a surface integral, and, as \( \Delta t \) goes to zero, the integrand value of F(x,t) within these elemental volumes may be taken as that of F on the surface \( A^*(t) \), thus:

\[ \int\limits_{\Delta V} F(\mathbf{x},t) dV \cong \int\limits_{A^*(t)} F(\mathbf{x},t) (\mathbf{b} \Delta t \cdot \mathbf{n}) dA \text{ as } \Delta t \to 0. \]
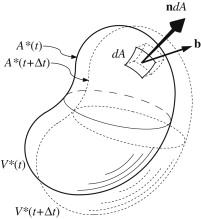
Graphical Control Volume

Geometrical depiction of a control volume \( V^*(t) \) having a surface \( A^*(t) \) that moves at a nonuniform velocity \( \mathbf{b} \) during a small time increment \( \Delta t \).

When \( \Delta t \) is small enough, the volume increment \( \Delta V = V^*(t+\Delta t) - V^*(t) \) will lie very near \( A^*(t) \), so the volume-increment element adjacent to \( dA \) will be \( (\mathbf{b} \Delta t) \cdot \mathbf{n} dA \) where \( \mathbf{n} \) is the outward normal on \( A^*(t) \).

◀ ▶