Material-isotropy and stress-symmetry restrictions. Substitution of \(K_{ijmn} = \lambda \delta_{ij} \delta_{mn} + \mu \delta_{im} \delta_{jn} + \gamma \delta_{in} \delta_{jm}\) into the constitutive \(\tau_{ij} = K_{ijmn} S_{mn}\) yields \[ \tau_{ij} = 2\mu S_{ij} + \lambda S_{mm} \delta_{ij} \] where \( S_{mm} = \nabla \cdot \mathbf{u} \) is the volumetric strain rate

The complete stress tensor \(\boxed{T_{ij} = -p \delta_{ij} + \tau_{ij}}\) then becomes \[ T_{ij} = -p \delta_{ij} + 2\mu S_{ij} + \lambda S_{mm} \delta_{ij} \] and this is the appropriate multidimensional extension of Newton’s law of viscous friction

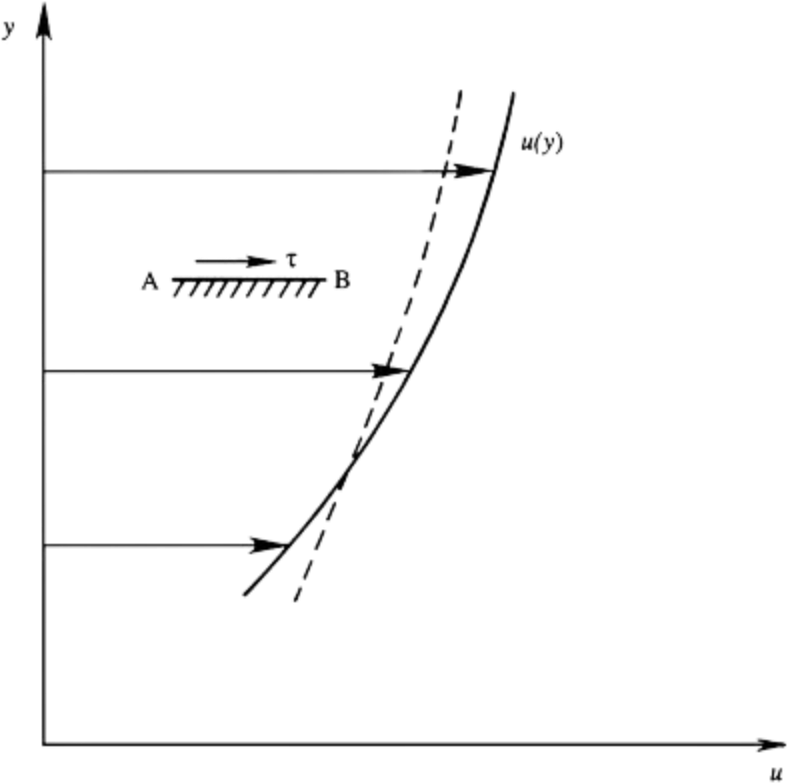
From high to low \( u \), is equivalent to a shear stress, \( \tau \) existing in the fluid. Experiments show that the magnitude of \( \tau \) along a surface such as AB is to a good approximation proportional to the local velocity gradient \[ \tau = \mu \left( \frac{du}{dy} \right) \] where the constant of proportionality \( \mu \) (with units of kg m\(^{-1}\) s\(^{-1}\)) is known as the dynamic viscosity. This is Newton’s law of viscous friction. The diffusive action of fluid viscosity tends to decrease velocity gradients, so that the continuous line tends toward the dashed line

The two scalar constants \( \mu \) and \( \lambda \) can be further related. Setting \( i = j \), summing over the repeated index, and noting that \( \delta_{ii} = 3 \) obtain \[ T_{ii} = -3p + (2\mu + 3\lambda) S_{mm} \] from which the pressure is found to be \[ p = -\tfrac{1}{3} T_{ii} + \left( \tfrac{2}{3} \mu + \lambda \right) \nabla \cdot \mathbf{u} \] The diagonal terms of \( T_{ij} \) in a flow may be unequal because of the term proportional to \( \mu \) in \(T_{ij} = -p \delta_{ij} + 2\mu S_{ij} + \lambda S_{mm} \delta_{ij}\) and the fact that the diagonal terms of \( S_{ij} \) in a flow may be unequal

◀ ▶