For the stress tensor \(\mathbf{T}\), the first index of \( T_{ij} \) indicates the direction of the normal to the surface on which the stress is considered, and the second index indicates the direction in which the stress acts. The diagonal elements \( T_{11}, T_{22}, \) and \( T_{33} \) of the stress matrix are the normal stresses, and the off-diagonal elements are the tangential or shear stresses

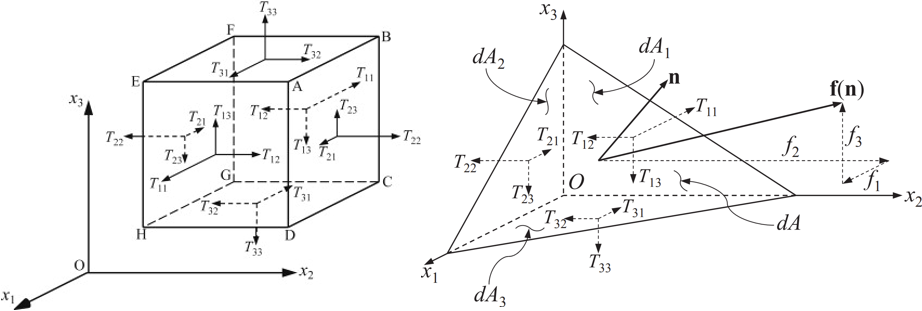
The figure shows the directions of positive stresses on the various faces of small cubical and tetrahedral fluid elements. Denoting the cubical volume by \( dV = dx_1 dx_2 dx_3 \) and considering the torque produced on it by the various stresses components, it can be shown that the stress tensor is symmetric \[ T_{ij} = T_{ji} \]

By considering the element’s rotational dynamics in the limit \( dV \rightarrow 0 \), the stress tensor has only six independent components. However, this symmetry is violated if there are body-force couples proportional to the mass of the fluid element (such as those exerted by an electric field on polarized fluid molecules). Antisymmetric stresses must be included in such circumstances

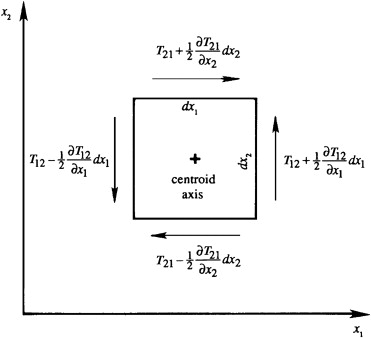
[Q] Prove that the stress tensor is symmetric by considering first-order changes in surface forces on a vanishingly small cube in rotational equilibrium. Work with rotation about the number 3 coordinate axis to show \( T_{12} = T_{21} \). Cyclic permutation of the indices will suffice for showing the symmetry of the other two shear stresses
[Pf] Rotational equilibrium about an axis through the cube's center parallel to the \(x_3\) axis requires \( + \left[ T_{12} + \frac{\partial T_{12}}{\partial x_1} \frac{dx_1}{2} \right] \left( dx_2 dx_3 \right) \frac{dx_1}{2} + \left[ T_{12} - \frac{\partial T_{12}}{\partial x_1} \frac{dx_1}{2} \right] \left( dx_2 dx_3 \right) \frac{dx_1}{2} \\ - \left[ T_{21} + \frac{\partial T_{21}}{\partial x_2} \frac{dx_2}{2} \right] \left( dx_1 dx_3 \right) \frac{dx_2}{2} - \left[ T_{21} - \frac{\partial T_{21}}{\partial x_2} \frac{dx_2}{2} \right] \left( dx_1 dx_3 \right) \frac{dx_2}{2} + \text{higher order terms} \\ = \frac{\rho}{12} dx_1 dx_2 dx_3 \left\{ (dx_1)^2 + (dx_2)^2 \right\} \frac{d\Omega}{dt} \)
\( \Omega \) is the rotation rate, the first 4 terms are written as triple products (surface stress)(surface area)(moment arm). The final term is the product of the moment of inertia about the \(x_3\)-axis and the rotational acceleration

Canceling terms and dividing by \(dV\) produces \(\boxed{ T_{12} - T_{21} = \frac{\rho}{12} \left\{ (dx_1)^2 + (dx_2)^2 \right\} \frac{d\Omega}{dt}} \) Taking \( dx_1, dx_2 \to 0 \), produces \( \tau_{12} = \tau_{21} \). Cyclic permutation of the indices can be used to show the equality of the other two shear stresses: \( T_{23} = T_{32} \), and \( T_{31} = T_{13} \)

¹\( \underbrace{\left( T_{12} (dx_2 dx_3) \tfrac{dx_1}{2} + \cancel{ \tfrac{\partial T_{12}}{\partial x_1} \tfrac{dx_1}{2} (dx_2 dx_3) \tfrac{dx_1}{2} } + T_{12} (dx_2 dx_3) \tfrac{dx_1}{2} - \cancel{ \tfrac{\partial T_{12}}{\partial x_1} \tfrac{dx_1}{2} (dx_2 dx_3) \tfrac{dx_1}{2} } \right)}_{\text{Faces normal to } x_1} - \underbrace{\left( T_{21} (dx_1 dx_3) \tfrac{dx_2}{2} + \cancel{ \tfrac{\partial T_{21}}{\partial x_2} \tfrac{dx_2}{2} (dx_1 dx_3) \tfrac{dx_2}{2} } + T_{21} (dx_1 dx_3) \tfrac{dx_2}{2} - \cancel{ \tfrac{\partial T_{21}}{\partial x_2} \tfrac{dx_2}{2} (dx_1 dx_3) \tfrac{dx_2}{2} } \right)}_{\text{Faces normal to } x_2} = T_{12} dx_1 dx_2 dx_3 - T_{21} dx_1 dx_2 dx_3 = (T_{12} - T_{21}) dx_1 dx_2 dx_3 \)

◀ ▶