Conservation of Momentum

The body force \( \rho \mathbf{g} dV \) acting on the fluid element \( dV \) does so without physical contact. Body forces commonly arise from gravitational or electromagnetic force fields. In addition, in accelerating or rotating frames of reference, fictitious body forces arise from the frame’s noninertial motion. By definition body forces are distributed through the fluid and are proportional to mass (or electric charge, electric current, etc.)
Body forces may be conservative or nonconservative.

Conservative body forces are those that can be expressed as the gradient of a potential function \[ \mathbf{g} = -\nabla \Phi \quad \text{or} \quad g_j = - \partial \Phi / \partial x_j \]
\( \Phi \) is called the force potential; it has units of energy per unit mass. When the \( z \)-axis points vertically upward, the force potential for gravity is \( \Phi = gz \), where \( g \) is the acceleration of gravity, and \(\boxed{\mathbf{g} = -\nabla \Phi \quad \text{or} \quad g_j = - \partial \Phi / \partial x_j}\) produces \( \mathbf{g} = -g \mathbf{e}_z \); forces satisfying it are called conservative because the work done by conservative forces is independent of the path, and the sum of fluid-particle kinetic and potential energies is conserved when friction is absent

Surface forces \(\mathbf{f}\) act on fluid elements through direct contact with the surface of the element. They are proportional to the contact area and carry units of stress (force per unit area). Surface forces are commonly resolved into components normal and tangential to the contact area.

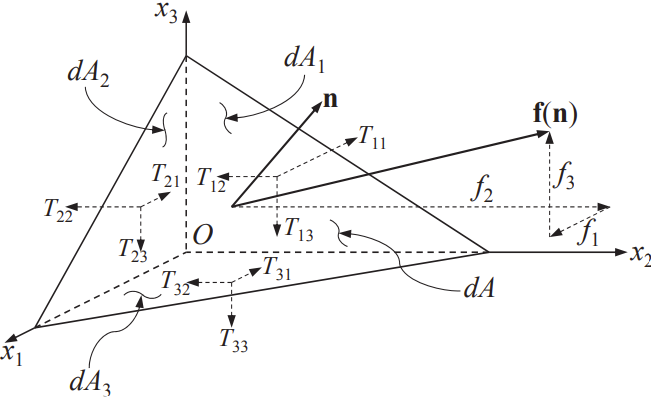
TensorTetrahedralElement

Consider an arbitrarily oriented element of area \(dA\) in a fluid. The net force \( f_1 \) on the element in the first direction produced by the stresses \( T_{ij} \) is \(\boxed{ f_1 \, dA = T_{11} \, dA_1 + T_{21} \, dA_2 + T_{31} \, dA_3} \). If \(\mathbf{n}\) is the surface normal with components \(n_i\), then from \(\boxed{ f_i = \sum_{j=1}^{3} T_{ji} n_j \equiv T_{ji} n_j \quad \text{or} \quad \mathbf{f} = \mathbf{n} \cdot \mathbf{T}} \) the components \(f_j\) of the surface force per unit area \(\mathbf{f}(\mathbf{n}, \mathbf{x}, t)\) on this element are \( f_j = n_i T_{ij} \) where \(T_{ij}\) is the stress tensor. Thus, the normal component of \(\mathbf{f}\) is \(\mathbf{n} \cdot \mathbf{f} = n_i f_i\), while the tangential component is the vector \(\mathbf{f} - (\mathbf{n} \cdot \mathbf{f}) \mathbf{n}\) which has components \( f_k - (n_i f_i) n_k \)

◀ ▶