Leibniz's Theorem & Reynolds Transport Theorem

Leibniz's Theorem:

\[ \frac{d}{dt} \int_{a(t)}^{b(t)} F(x,t) dx = \int_{a}^{b} \frac{\partial F}{\partial t} dx + \frac{db}{dt} F(b,t) - \frac{da}{dt} F(a,t) \]

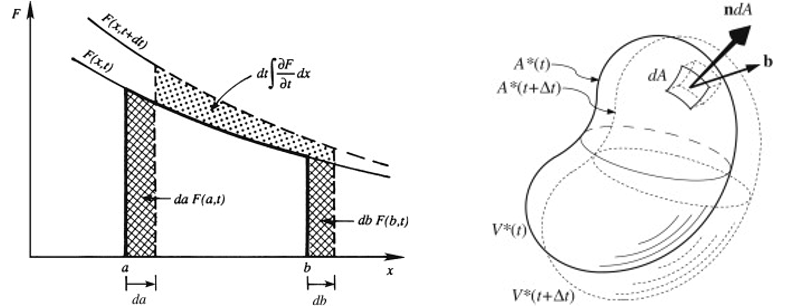
A geometrical generalization of Leibniz’s rule is presented using control volumes.

\[ \frac{d}{dt} \int_{V^*(t)} F(x,t) dV = \lim_{\Delta t \to 0} \frac{1}{\Delta t} \left\{ \int_{V^*(t+\Delta t)} F(x,t+\Delta t) dV - \int_{V^*(t)} F(x,t) dV \right\} \]