Divergence of a Vector Field:
\[ \text{div}\, \mathbf{u} = \frac{\partial u_1}{\partial x} + \frac{\partial u_2}{\partial y} + \frac{\partial u_3}{\partial z} = \left( \frac{\partial}{\partial x}, \frac{\partial}{\partial y}, \frac{\partial}{\partial z} \right) \cdot (u_1, u_2, u_3) = \nabla \cdot \mathbf{u} \]
Curl of a Vector Field:
\[ \text{curl } \mathbf{u} = \left( \frac{\partial u_3}{\partial y} - \frac{\partial u_2}{\partial z}, \; \frac{\partial u_1}{\partial z} - \frac{\partial u_3}{\partial x}, \; \frac{\partial u_2}{\partial x} - \frac{\partial u_1}{\partial y} \right) = \begin{vmatrix} \mathbf{e}_1 & \mathbf{e}_2 & \mathbf{e}_3 \\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\ u_1 & u_2 & u_3 \end{vmatrix} = \nabla \times \mathbf{u}\]
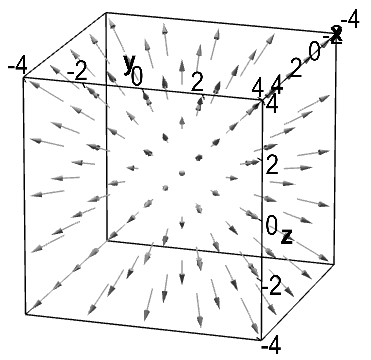
Divergent vector field
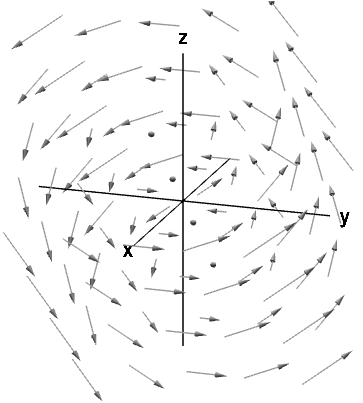
A rotating vector field
1Divergence and curl example:
https://mathinsight.org/divergence_curl_examples
2P. C. Matthews, Vector Calculus, New York:Springer-Verlag, 1998.