A two-dimensional, or plane, flow is one in which the variation of flow characteristics can be described by two spatial coordinates. The flow of an ideal fluid past a circular cylinder of infinite length having its axis perpendicular to the primary flow direction is an example of a plane flow. This definition of two-dimensional flow officially includes the flow around bodies of revolution where flow characteristics are identical in any plane that contains the body’s axis. However, such flows are customarily called three-dimensional axisymmetric flows.

A three-dimensional flow is one that can only be properly described with three independent spatial coordinates and is the most general case considered in this text. Sometimes curvilinear coordinates that match flow-field boundaries or symmetries greatly simplify the analysis and description of flow fields.

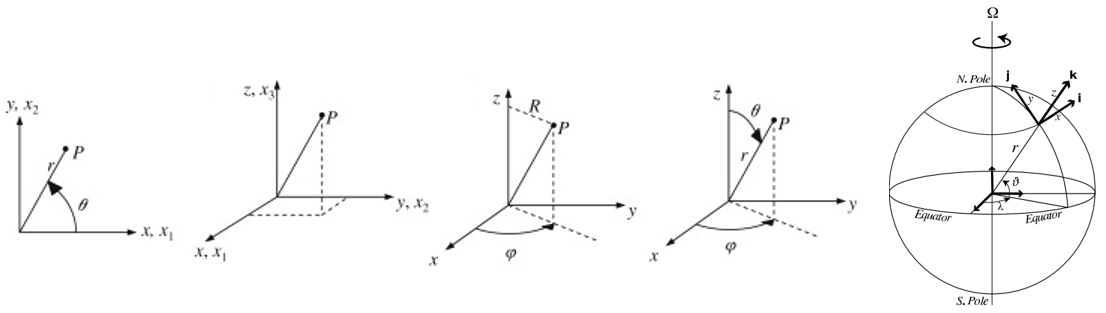
Several different coordinate systems are used. Two-dimensional (plane) Cartesian and polar coordinates for an arbitrary point P may be denoted by the coordinate pairs \((x,y)\), \((x_1,x_2)\), or \((r, \theta)\) with the corresponding velocity components \((u, v)\), \((u_1, u_2)\), or \((u_r, u_\theta)\).

In three dimensions, Cartesian coordinates may be used to locate a point P via the coordinate triplets \((x,y,z)\) or \((x_1,x_2,x_3)\) with corresponding velocity components \((u, v, w)\) or \((u_1, u_2, u_3)\).