Stokes’s theorem gives an alternative expression for the surface integral of the curl of a vector field. This is analogous to the divergence theorem, so Stokes’s theorem could be referred to as the ‘curl theorem’. The proof of the theorem is very similar to that for the divergence theorem, being based on the definition of curl in terms of a line integral
Let \( C \) be a closed curve which forms the boundary of a surface \( S \). Then for a continuously differentiable vector field \( \mathbf{u} \), Stokes’s theorem states that
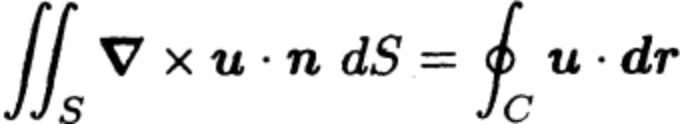
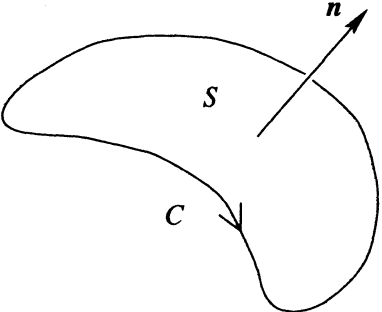
The direction of the line integral around \( C \) and the normal \( \mathbf{n} \) are oriented in a right-handed sense
1P. C. Matthews, Vector Calculus, New York:Springer-Verlag, 1998.