Proof
Now take the limit \( \delta V_i \rightarrow 0 \). The l.h.s. becomes the volume integral
of \( \nabla \cdot \mathbf{u} \) over the volume \( V \); this is just the definition of
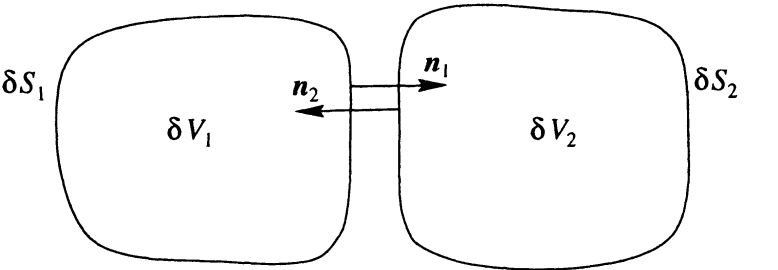
the volume integral. To simplify the r.h.s. consider two adjacent volume elements \( \delta V_1 \)
and \( \delta V_2 \)
Since the normal vector to each surface points outward, the normal vectors to the two surfaces
along their common surface point in opposite directions: \( \mathbf{n}_1 = -\mathbf{n}_2 \).
Therefore the values of \( \mathbf{u} \cdot \mathbf{n} \) cancel along the common surface:
\( \mathbf{u} \cdot \mathbf{n}_1 + \mathbf{u} \cdot \mathbf{n}_2 = 0 \)
This means that all the contributions to the sum on the r.h.s. of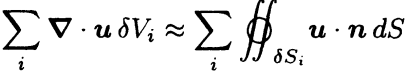 
from the interior of the region \( V \) cancel out, leaving only the surface integral over the exterior surface \( S \).
So in the limit \( \delta V_i \rightarrow 0 \), 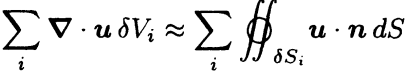becomes
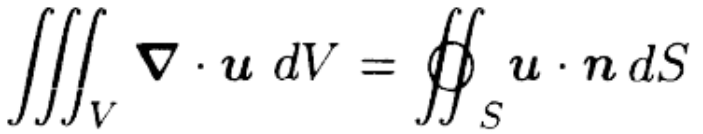
1P. C. Matthews, Vector Calculus, New York:Springer-Verlag, 1998.