A tensor B is called symmetric in the indices \( i \) and \( j \) if the components do not
change when \( i \) and \( j \) are interchanged, that is, if \( B_{ij} = B_{ji} \)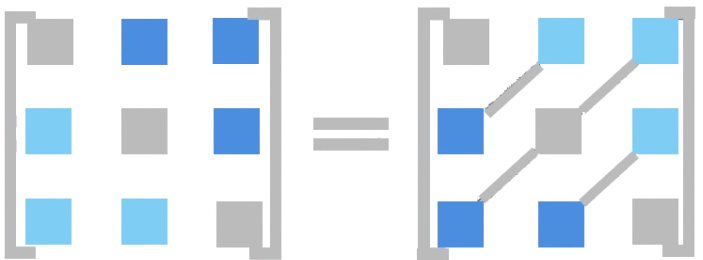
.
Thus, the matrix of a symmetric second-order tensor is made up of only six distinct components
(the three on the diagonal where \( i = j \), and the three above or below the diagonal
where \( i \ne j \)). On the other hand, a tensor is called antisymmetric
if \( B_{ij} = -B_{ji} \) 
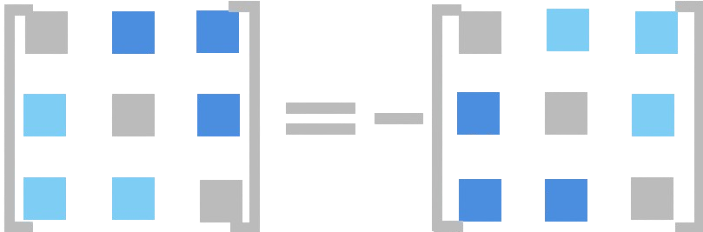. An antisymmetric tensor's diagonal components are each zero, and it
has only three distinct components (the three above or below the diagonal).
Any tensor can be represented as the sum of symmetric and antisymmetric tensors. If we write:
\[
B_{ij} = \frac{1}{2}(B_{ij} + B_{ji}) + \frac{1}{2}(B_{ij} - B_{ji}) = S_{ij} + A_{ij}
\]
then the operation of interchanging \( i \) and \( j \) does not change the first term,
but changes the sign of the second term.
Therefore, \( (B_{ij} + B_{ji})/2 \equiv S_{ij} \) is called
the symmetric part of \( B_{ij} \), and \( (B_{ij} - B_{ji})/2 \equiv A_{ij} \) is called the
antisymmetric part of \( B_{ij} \)
\[ A_{ij} = \frac{1}{2} \underbrace{(A_{ij} + A_{ji})}_{E_{ij}} + \frac{1}{2} \underbrace{(A_{ij} - A_{ji})}_{\Omega_{ij}} \] You can easily check that \( E_{ij} \) is symmetric \( (E_{ij} = E_{ji}) \) and \( \Omega_{ij} \) is antisymmetric \( (\Omega_{ij} = -\Omega_{ji}) \)
Now let’s try this recipe on our velocity gradient tensor \( A_{ij} = (\nabla \vec{V}) = \partial_i v_j \) and decompose it into symmetric and antisymmetric parts. We will have \[ A_{ij} = \frac{1}{2} \underbrace{(\partial_i v_j + \partial_j v_i)}_{E_{ij}} + \frac{1}{2} \underbrace{(\partial_i v_j - \partial_j v_i)}_{\Omega_{ij}} \]