Einstein Summation Notation

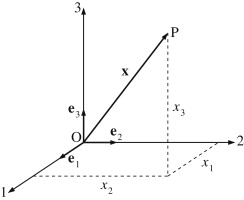
Vectors and Tensors: Vectors and first-order tensors have both a magnitude and a direction. A vector can be completely described by its components along three orthogonal coordinate directions. The components of a vector may change with a change in the coordinate system, and vectors are typically denoted using boldface symbols.

Common vectors in fluid mechanics include position \( \mathbf{x} \), fluid velocity \( \mathbf{u} \), and gravitational acceleration \( \mathbf{g} \). In a Cartesian coordinate system with unit vectors \( \mathbf{e_1}, \mathbf{e_2}, \mathbf{e_3} \), the position vector is expressed as \( \mathbf{x} = x_1 \mathbf{e_1} + x_2 \mathbf{e_2} + x_3 \mathbf{e_3} \).

The transpose of a vector swaps its row and column representation: \( \mathbf{x}^{\top} = [x_1 \quad x_2 \quad x_3] \).

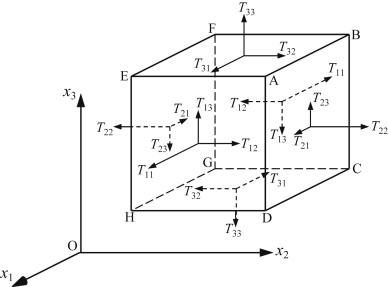
Second-order tensors extend these concepts to pairs of coordinate directions, such as the stress tensor \( \mathbf{T} \), which has nine components in three-dimensional space.

The Einstein summation convention is a compact way to represent summation over repeated indices in tensor notation.

Implicit Summation: This convention states that whenever an index is repeated in a term, a summation over that index is implied, even though no summation sign is explicitly written.

The dot product of two vectors \( \mathbf{u} \) and \( \mathbf{v} \) is written as: \( \mathbf{u} \cdot \mathbf{v} = v \cdot u = u_1 v_1 + u_2 v_2 + u_3 v_3 = \sum_{i=1}^{3} u_i v_i \equiv u_i v_i \).

This notation reduces writing complexity and increases mathematical precision, especially in expressions involving vectors, tensors, and higher-order equations. It is widely used in physics and engineering for fluid mechanics, relativity, and continuum mechanics, simplifying complex tensor equations.