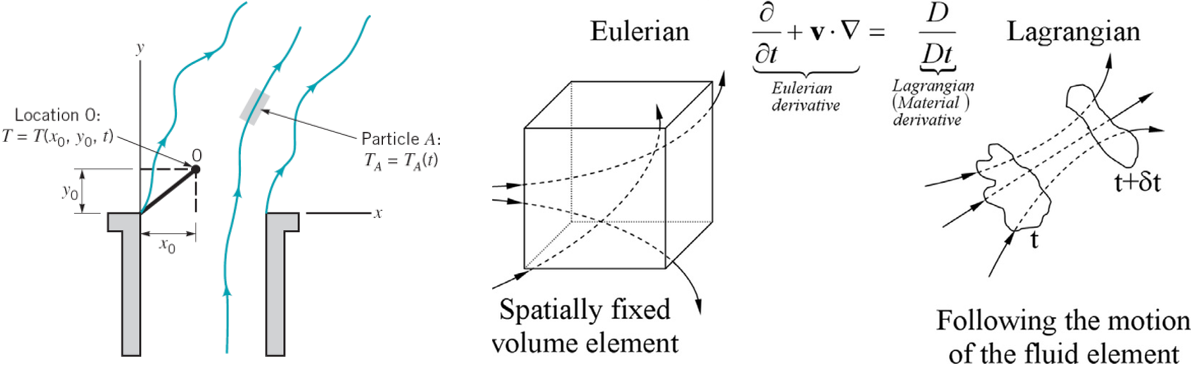
These equations are useful for computing the acceleration of a fluid particle anywhere in a flow from the velocity field (a function of \( x, y, z, \) and \( t \)); this is the Eulerian method of description, the most-used approach in fluid mechanics. Plus, we will use these acceleration descriptions to construct Newton’s law of motion for fluids (remember that right now we are just using kinematics and have not talked about forces in the fluids yet. So, so far we only have the \( a \) in the \( F = ma \)).

As an alternative (e.g., if we wish to track an individual particle’s motion in, for example, pollution studies), we sometimes use the Lagrangian description of particle motion, in which the acceleration, position, and velocity of a particle are specified as a function of time only. Both descriptions are illustrated in the example we solved in the class.